I have always had problems in understanding deep and complex recusion eventhough they all follow a common pattern that is There is always a base case to stop the recursion and making a recursive call on some smaller part of the solution, I decided to set my bar high . Here are the things i set to use recursion to understand complex recursive calls .
- Solving Sudoku using Backtracking
- The Chess Knight - Queen classic
- Permutations
- More problems as I come across.
Let start with the case that allows you to select all possible combinations of all members a set. I learnt that this recursive pattern in very important to understand because the is a common pattern used in solving the problems that I mentioned above and many others like searching and solving word puzzles
Permutation
I define permutations as all the ways to arrange a set of items for example if you permute the word {cat} you get {cat, tac, act, atc, tca, cta}. Permutations are mathematical and if you want a deeper understanding of this then go to Permutation. in Wikepidia and read more
In the program below the program does permutation recursively . I am writing this because I feel I have started getting the power of recursion and how to solve problems with them. The truth is i understood the classical recursive examples in the university like Fibonacci ,factorials and the towers of Hanoi but when it came to complex recursive example like the one below. I got a headache in thinking recursively.
Here are the tough questions to answer when writing a program that does permutations.
- How do you just pick one element on the set and know which one to attach next?
- How do you avoid doubles and repeating each elements?
- How do you separate them?
- How do you know that all the possible combinations of the set have been made?
Here is the program written in C# that does permutations .
class Program
{
static void Main(string[] args)
{
Permutate("ABCD");
}
public static void RecPermute(string permutateHolder , string itemToPermutate)
{
if (itemToPermutate== string.Empty)
{
Console.WriteLine(permutateHolder);
}
else
{
for (int i = 0; i < itemToPermutate.Length; i++)
{ // Get the rest of the items remaining in the set
var remaining = itemToPermutate.Substring(0, i) + itemToPermutate.Substring(i+1);
//Take each element from the item and do a recursive call on them
RecPermute(permutateHolder + itemToPermutate[i], remaining);
}
}
}
// Wrapper for permutate function
public static void Permutate(string item)
{
RecPermute("", item);
}
}
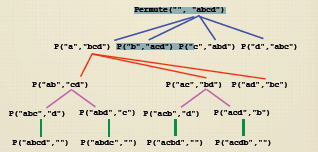
Here is part of the recursive tree of the program Permutate("ABCD").It show permutations for all elements beginning with the letter A.The other elements of the set follow the same pattern.
Happy programming !